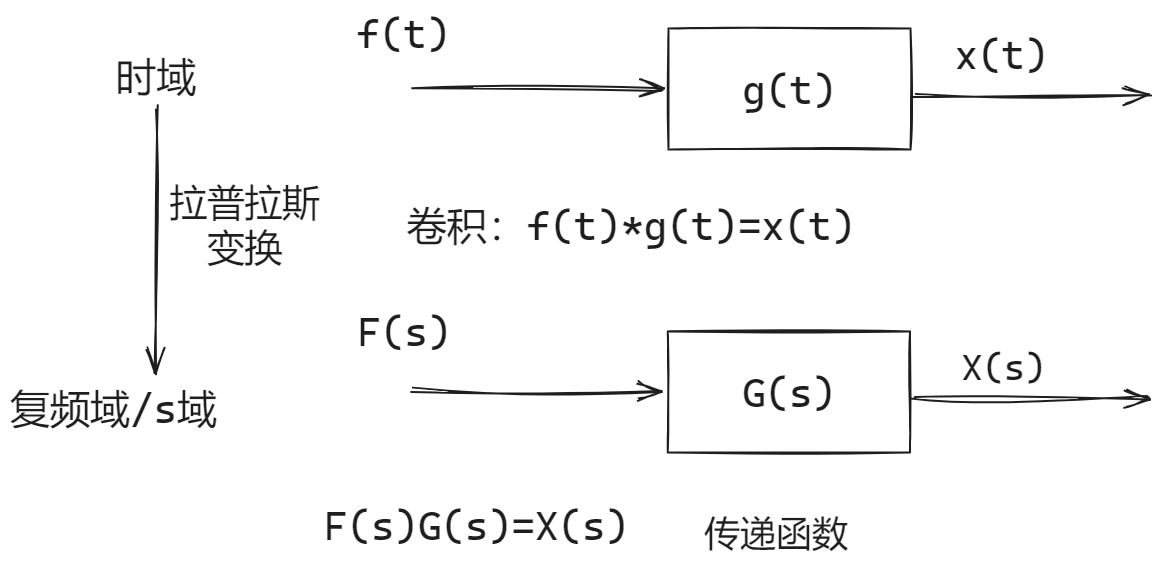
传递函数
Transform Fuction
复变量的有理分式函数
- 使用系统参数表示输出量与输入量之间关系的表达式
- 只取决于系统或元件的结构与参数,表征了系统本身的动态特性
- 输出(果)= 输入(因)
- 与微分方程对应
一个 就是一个微分算子
线性时不变系统中,定义为:
零初始条件下,系统输出量与输入量的拉普拉斯变换之比
一、传递函数标准形式
1. 首 1 标准型
零极点形式,常见于根轨迹法基础:
为根轨迹增益
2. 尾 1 标准型
常见于频域分析法
为时间常数 为传递函数系数/系统的增益 - 传递函数分母为特征方程
二、极点与零点
零极点
极点:分母多项式的解 ×
特征方程的根(特征根),可以受输入函数的激发,在输出响应中形成自由运动的模态
如果有极点
零点:分子多项式的解 O
不形成自由运动的模态,但是影响各模态在响应中所占的比重,影响响应曲线的形状
注意
- 零点、极点、原点三者之间的距离共同影响响应曲线
- 实际上,非零初始条件不会影响系统的传递函数,非零的输入与实际输入量满足叠加原理
三、传递函数的计算
基本传函
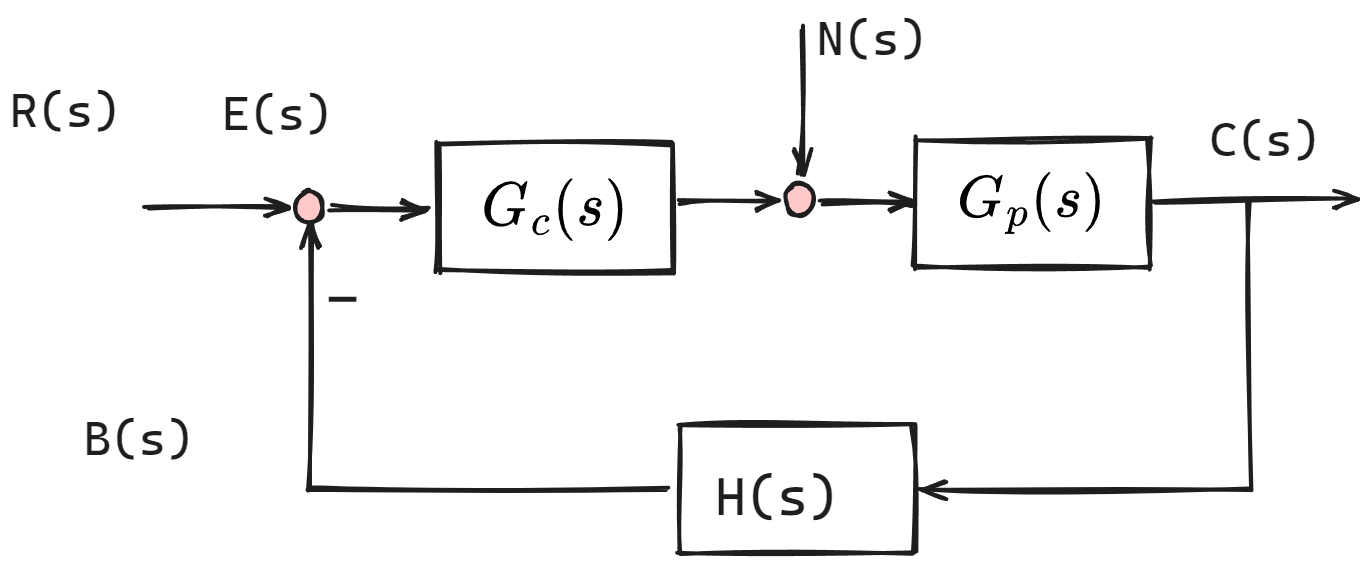
- 前向通路传递函数:输入端到输出端的通路的传递函数的乘积 (看输入和输出信号)
- 开环传递函数:打开主反馈回路,主反馈信号与误差信号之比 (与输入信号无关,由系统本身结构决定)
- 闭环传递函数:
- 误差传递函数:误差信号与输入信号之比
求传递函数的方法
四、时间响应
已知传递函数
一般给定输入为经典输入信号,求时间响应:主要使用拉普拉斯变换#6.极限性质
五、经典环节的传递函数
RLC 电路
电路元件的传递函数
-
电阻:
-
电容:
-
电感:
复数阻抗法:列写网络的微分方程时,由于流过电流相同。可以直接将输出电压和输入电压的比值,直接列写出传函,再拉普拉斯逆变换,求时域的微分关系
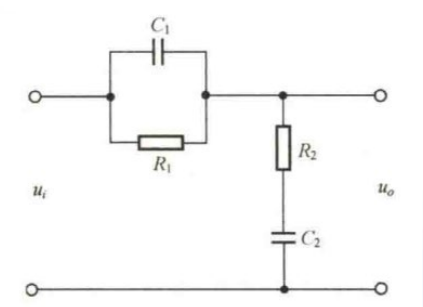
例题
- 并联/串联电路的复数阻抗类似于求电阻
- 类似于分压原理求最后传函
六、非零初始条件的传递函数
基本流程
- 先根据系统结构,得到零初始条件下的传递函数
- 根据拉普拉斯逆变换,写出传递函数对应的微分方程
(注意“输出=输入”,输出在左,输入在右) - 再进行拉普拉斯变换,得到非零初始条件下的传递函数
注意使用带初值的微分性质
- 最后拉普拉斯逆变换:求有初值的时间响应
例题
控制系统传递函数为:
-
已有传递函数:
-
拉式逆变换,对应的微分方程:
-
拉氏变换,得到有初值的传递函数:
- 拉普拉斯逆变换,得到时间响应:
求时间响应